Author: Bárbara Barros

This week we have a guest blog post from Bárbara Barros Carlos, PhD candidate at DIAG Robotics Lab. Enjoy!

Quadrotors are characterized by their underactuation, nonlinearities, bounded inputs, and, in some cases, communication time-delays. The development of their maneuvering capability poses some challenges that cover dynamics modeling, state estimation, trajectory generation, and control. The latter, in particular, must be able to exploit the system’s nonlinear dynamics to generate complex motions. However, the presence of communication time-delay is known to highly degrade control performance.

In our recent work, we present an efficient position control architecture based on real-time nonlinear model predictive control (NMPC) with time-delay compensation for quadrotors. Given the current measurement, the state is predicted over the delay time interval using an integrator and then passed to the NMPC, which takes into account the input bounds. We demonstrate the capabilities of our architecture using the Crazyflie 2.1 nano-quadrotor.

Time-Delay Compensation

In our aerial system, because of the radio communication latency, we have delays both in receiving measurements and sending control inputs. Likewise, since we intend to use NMPC, the potentially high computational burden associated with its solution becomes an element that must also be taken into account to minimize the error in the state prediction.

To tackle this issue, we use a state predictor based on the round-trip time (RTT) associated with the sum of network latencies as a delay compensator. The prediction is computed by performing forward iterations of the system dynamic model, starting from the current measured state and over the RTT, through an explicit Runge Kutta 4th order (ERK4) integrator. Due to the independent nature of this operation, perfect delay compensation can be achieved by adjusting the integration step to be equal to the RTT. Thus, it is assumed that there is a fixed RTT, defined by τr, to be compensated.

Nonlinear Model Predictive Control

The NMPC controller is defined as the following constrained nonlinear program (NLP):

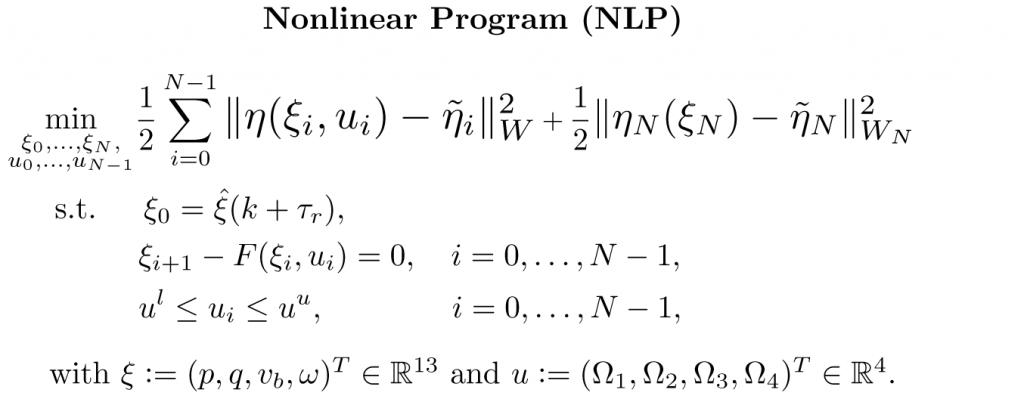
Therein, p denotes the inertial position, q the attitude in unit quaternions, vb the linear velocity expressed in the body frame, ω the angular rate, and Ωi the rotational speed of the i^th propeller. The NLP is tailored to the Crazyflie 2.1 and is implemented using the high-performance software package acados, which solves optimal control problems and implements a real-time iteration (RTI) variant of a sequential quadratic programming (SQP) scheme with Gauss-Newton Hessian approximation. The quadratic subproblems (QP) arising in the SQP scheme are solved with HPIPM, an interior-point method solver, built on top of the linear algebra library BLASFEO, finely tuned for multiple CPU architectures. We use a recently proposed Hessian condensing algorithm particularly suitable for partial condensing to further speed-up solution times.

When designing an NMPC, choosing the horizon length has profound implications for computational burden and tracking performance. For the former, the longer the horizon, the higher the computational burden. As for the latter, in principle, a long prediction horizon tends to improve the overall performance of the controller. In order to select this parameter and achieve a trade-off between performance and computational burden, we implemented the NLP in acados considering: five horizon lengths (N = {10,20,30,40,50}), input bounds on the rotational speed of the propellers (lower bound = 0, upper bound = 22 krpm), discretizing the dynamics using an ERK4 integration scheme. Likewise, we compare the condensing approach with the state-of-the-art solver qpOASES against the partial condensing approach with HPIPM, concerning the set of horizons regarded.

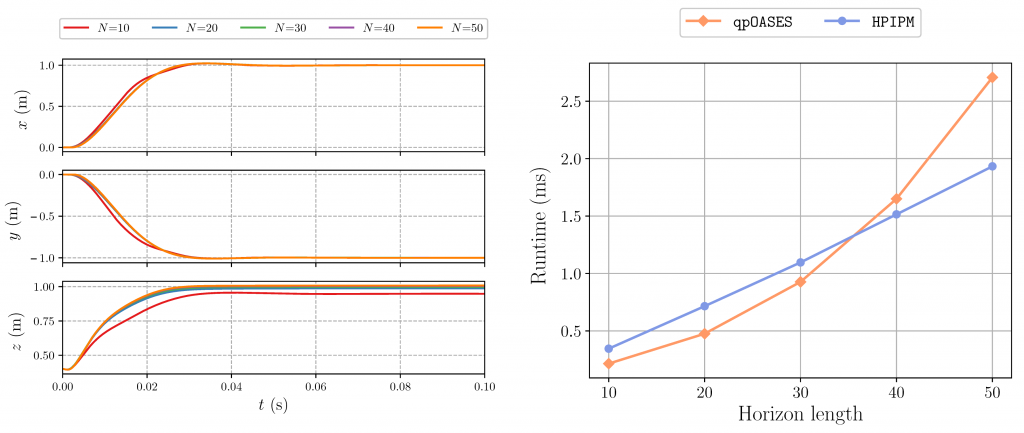
**Left: closed-loop trajectories comparing different horizon lengths.**
Right: average runtimes per SQP-iteration
for different horizon lengths considering two distinct QP solvers.

As qpOASES is a solver based on active-set method, it requires condensing to be computationally efficient. In line with the observations found in the literature that condensing is effective for short to medium horizon lengths, we note that qpOASES is competitive for horizons up to approximately N = 30 when compared to HPIPM. The break-even point moves higher on the scale for longer horizons, mainly due to efficient software implementations that cover: (a) Hessian condensing procedure tailored for partial condensing, (b) structure-exploiting QP solver based on novel Riccati recursion, (c) hardware-tailored linear algebra library. Therefore, we chose horizon N = 50 as it offers a reasonable trade-off between deviation from the reference trajectory and computational burden.

Onboard Controller Considerations

How the onboard controllers (PIDs) use the setpoints of the offboard controller (NMPC) in our architecture is not entirely conventional and, thereby, deserves some considerations. First, the reference signals that the PID loops track do not fully correspond to the control inputs considered in the NMPC formulation. Instead, part of the state solution is used in conjunction with the control inputs to reconstruct the actual input commands passed as a setpoint to the Crazyflie. Second, a part of the reconstructed input commands is sent as a setpoint to the outer loop (attitude controller), and the other part is sent to the inner loop (rate controller). Furthermore, as the NMPC model does not include the PID loops, it does not truly represent the real system, even in the case of perfect knowledge of the physical parameters. As a consequence, the optimal feedback policy is distorted in the real system by the PIDs.

Closed-loop Position Control Performance

Our control architecture hinges upon a ROS Kinetic framework and runs at 66.67 Hz. The Crazy RealTime Protocol (CRTP) is used in combination with our crazyflie_nmpc stack to stream in runtime custom packages containing the required data to reconstruct the part of the measurement vector that depends on the IMU data. Likewise, the cortex_ros bridge streams the 3D global position of the Crazyflie, which is then passed through a second-order, discrete-time Butterworth filter to estimate the linear velocities.

To validate the effectiveness of our control architecture, we ran two experiments. For each experiment, we generate a reference trajectory on a base computer and pass it to our NMPC ROS node every τs = 15 ms. When generating the trajectories, we explicitly address the feasibility issue in the design process, creating two references: one feasible and one infeasible. In addressing this issue, we prove through experiments that the performance of the proposed NMPC is not degraded even when the nano-quadrotor attempts to track an infeasible trajectory, which could, in principle, make it deviate significantly or even crash.

Overall, we observe that the most challenging setpoints to be tracked are the positions in which, given a change in the motion, the Crazyflie has to pitch/roll in the opposite direction quickly. These are the setpoints where the distortion has the greatest influence on the system, causing small overshoots in position. The average solution time of the tailored RTI scheme using acados was obtained on an Intel Core i5-8250U @ 3.4 GHz running Ubuntu and is about 7.4 ms. This result shows the efficiency of the proposed scheme.

Outlook

In this work, we presented the design and implementation of a novel position controller based on nonlinear model predictive control for quadrotors. The control architecture incorporates a predictor as a delay compensator for granting a delay-free model in the NMPC formulation, which in turn enforces bounds on the actuators. To validate our architecture, we implemented it on the Crazyflie 2.1 nano-quadrotor. The experiments demonstrate that the efficient RTI-based scheme, exploiting the full nonlinear model, achieves a high-accuracy tracking performance and is fast enough for real-time deployment.