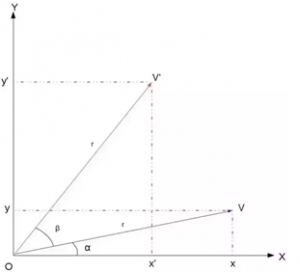
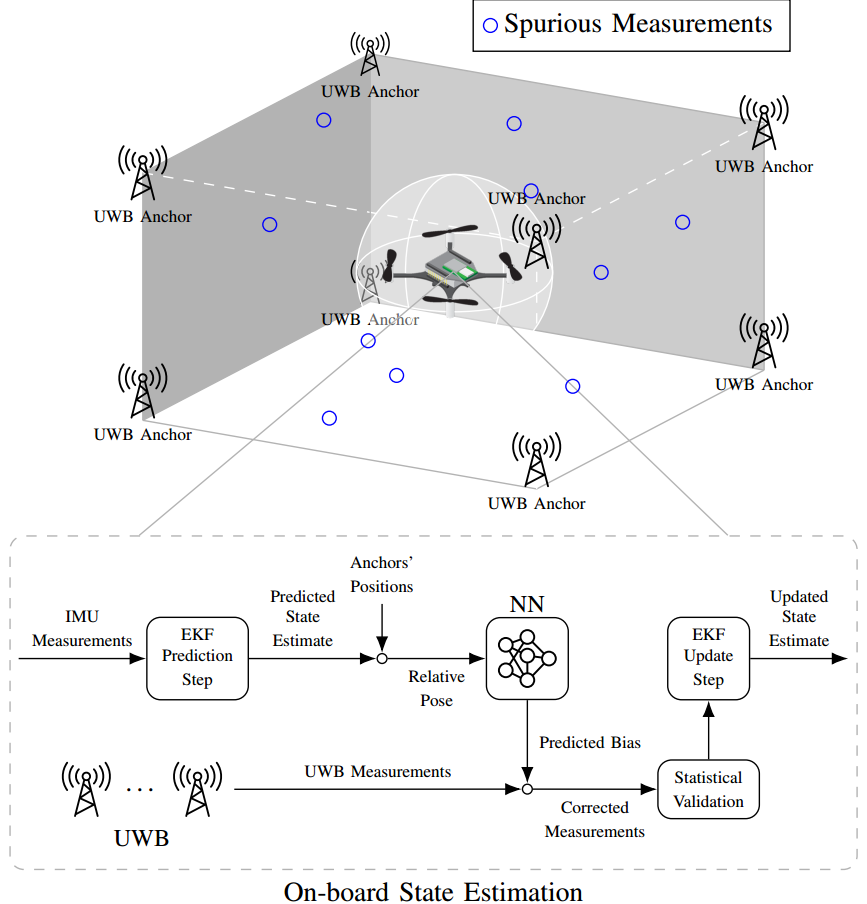
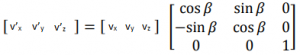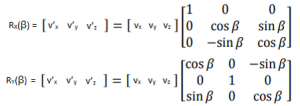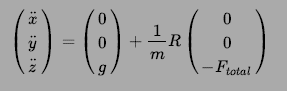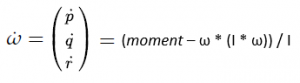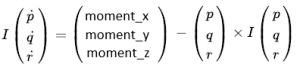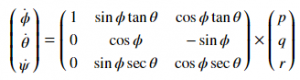Accurate indoor localization is a crucial enabling technology for many robotic applications, from warehouse management to monitoring tasks. Ultra-wideband (UWB) localization technology, in particular, has been shown to provide robust, high-resolution, and obstacle-penetrating ranging measurements. Nonetheless, UWB measurements are still corrupted by non-line-of-sight (NLOS) communication and spatially-varying biases due to doughnut-shaped antenna radiation pattern. In our recent work, we present a lightweight, two-step measurement correction method to improve the performance of both TWR and TDoA-based UWB localization. We integrate our method into the Extended Kalman Filter (EKF) onboard a Crazyflie and demonstrate a closed-loop position estimation performance with ~20cm root-mean-square (RMS) error.
Methodology
UWB measurement errors can be separated into two groups: (1) systematic bias caused by limitations in the UWB antenna pattern and (2) spurious measurements due to NLOS and multi-path propagation. We propose a two-step UWB bias correction approach exploiting machine learning (to address(1)) and statistical testing (to address (2)). The data-driven nature of our approach makes it agnostic to the origin of the measurement errors it corrects.
(1) Neural Network Bias Correction
The doughnut-shaped antenna radiation pattern causes the relative poses of anchors and tags to have a noticeable impact on the received signal power, which leads to systematic, predictable biases. To empirically demonstrate the systematic measurement errors resulting from varying the relative pose between anchors and tags, we placed two DWM1000 UWB anchors at a distance of 4m and collected both TWR and TDoA UWB range measurements for the UWB tag mounted on top of a Crazyflie spinning around its own z-axis.
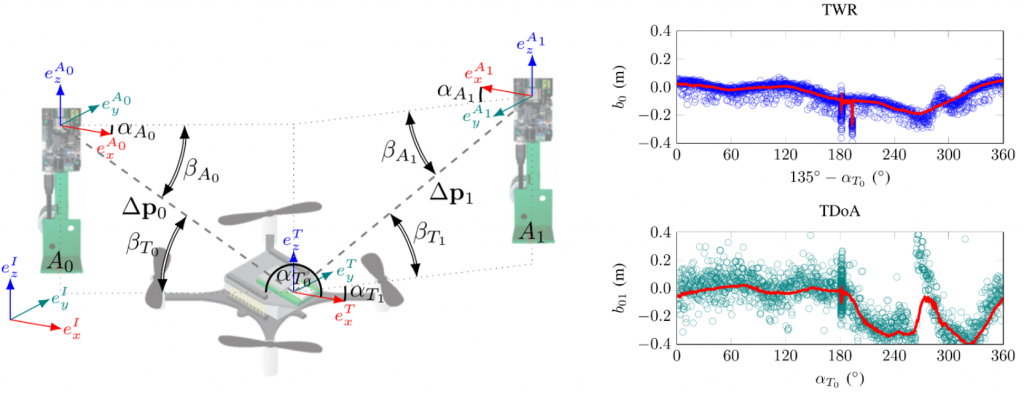
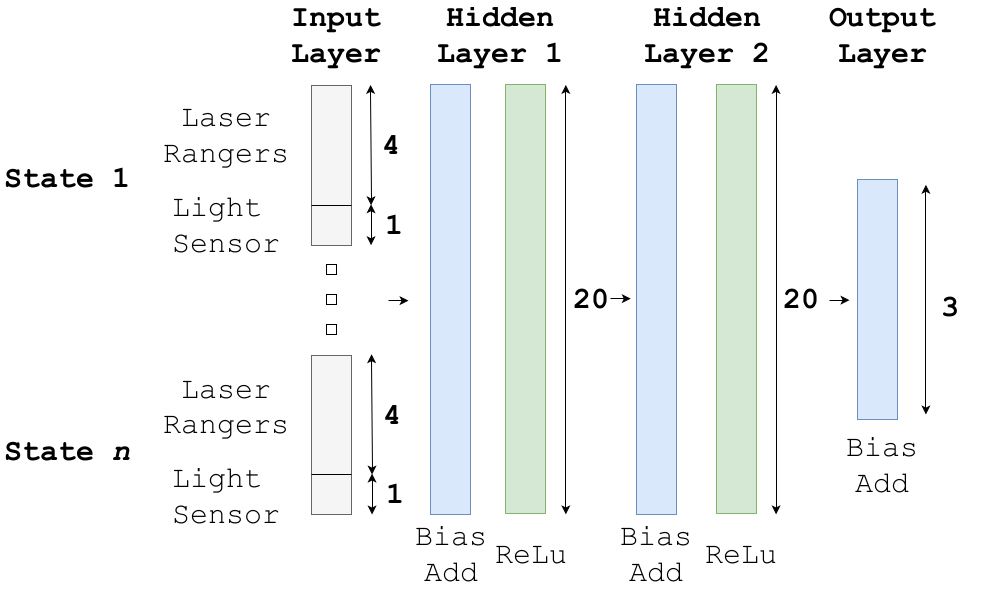
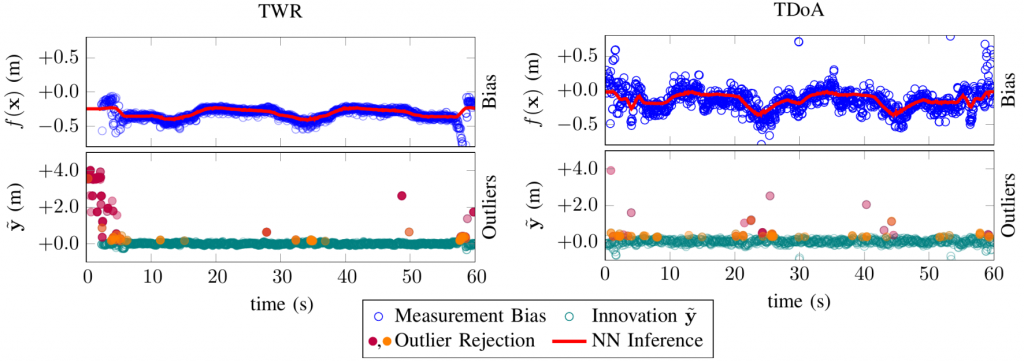
We choose to leverage the nonlinear representation power of neural networks to learn the systematic bias which only depends on anchor-tag relative poses. Considering the limited onboard computation power, we select a fully connected neural network with 50 neurons in each of two layers with ReLU activation. To represent the relative pose between the UWB tag and anchors, we select the relative distance ∆p and roll, pitch, and yaw angles of the quadcopter as the input features x for the network. As we used fixed anchors, we do not include their poses as inputs (this level of generalization is left for future work). Given sufficient training data, the spatially-varying measurement bias can be described by a nonlinear function b=f(x) captured by the trained neural network.
(2) Outlier (Spurious Measurements) Rejection
Besides our learning-based bias correction, we use a quadcopter’s dynamic model to filter inconsistent UWB range measurements. Given the estimated velocity v and maximum acceleration amax, we can compute the maximum distance dmax a quadcopter can cover during time ∆t. Based on this information, we can reject unattainable measurements before fusing them into the EKF by comparing the measurement innovation with dmax.
Moreover, we use a statistical hypothesis test to further classify potential outlier measurements. Since the measurement innovation vector is assumed to be distributed according to a multivariate Gaussian distribution, the normalized sum of squares of its values should follow a Chi-square distribution. We use the Chi-square hypothesis test to determine whether a measurement innovation is likely coming from this distribution.
Data Collection and Training
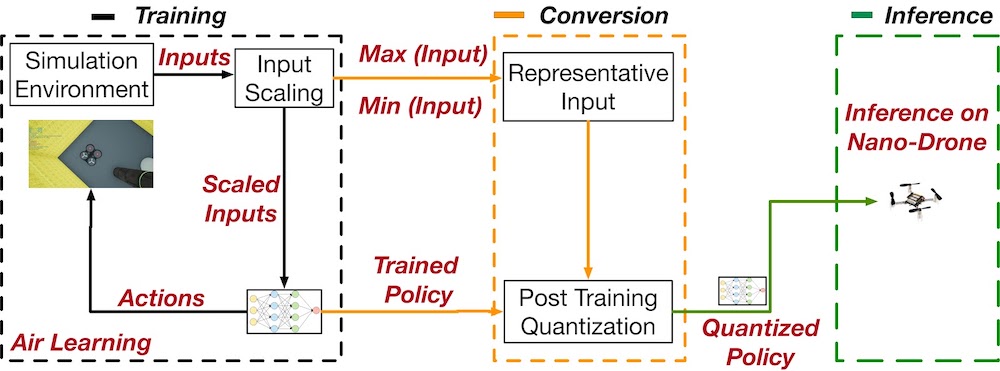
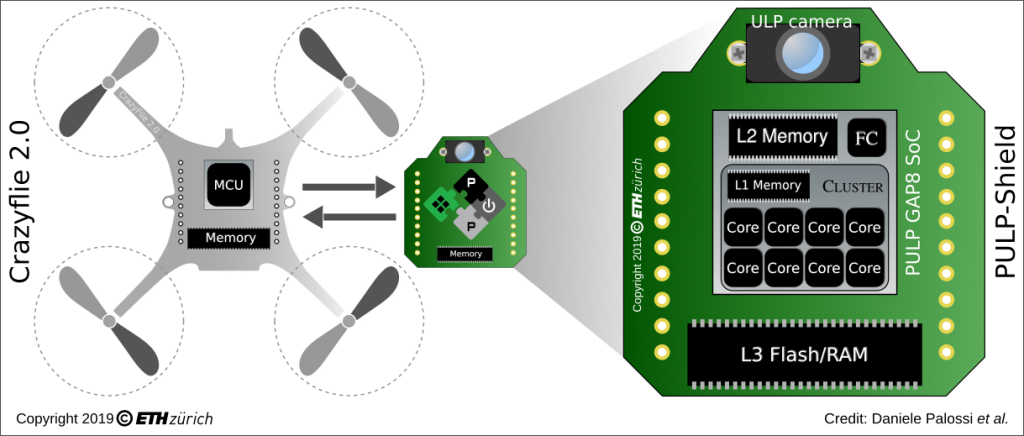
We use a Crazyflie 2.0 quadcopter and the Loco Positioning System (LPS)’s UWB DW1000 modules as our research platforms. Our calibration approach runs on the Crazyflie STM32 microcontroller within the FreeRTOS real-time operating system. We equipped a cuboid flying arena with 8 UWB anchors, one for each vertex. The anchor positions were measured using a Leica total station theodolite.
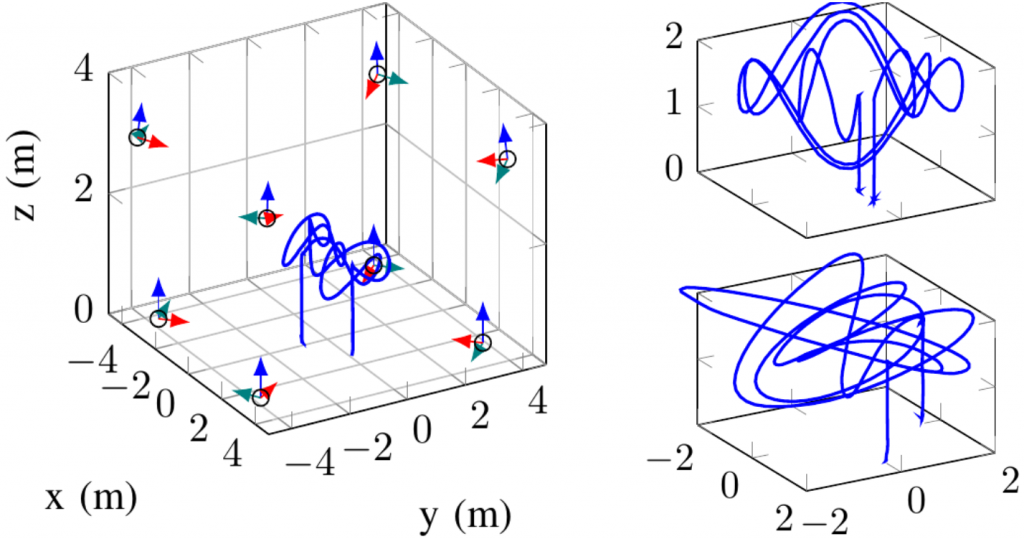
For all experiments, the ground truth position of the Crazyflie was provided by 10 Vicon cameras. The neural network was trained using PyTorch. To perform inference on the Crazyflie’s microcontroller, we re-use PyTorch’s trained weights in a plain C re-implementation. Since the DW1000 modules in the LPS provide UWB measurements every 5ms, the neural network inference runs at 200Hz during flight as well. Our outlier rejection method is also implemented in plain C and merged with the onboard EKF.
Close-loop Position Estimation Performance
We demonstrate the position estimation and close-loop performance of the proposed methods by flying a Crazyflie quadcopter along planar and non-planar circular trajectories (which were not among the trajectories used for training). A comparison between the estimation error of (A) the UWB localization estimate enhanced with outlier rejections and (B) the estimated enhanced with both outlier rejection and neural network bias compensation is conducted in our experiments for both TWR and TDoA2 modes. We repeated all of our experiments 10 times with a target velocity of 0.375m/s. The quadcopter trajectories during these flight tests are displayed in the following plots.
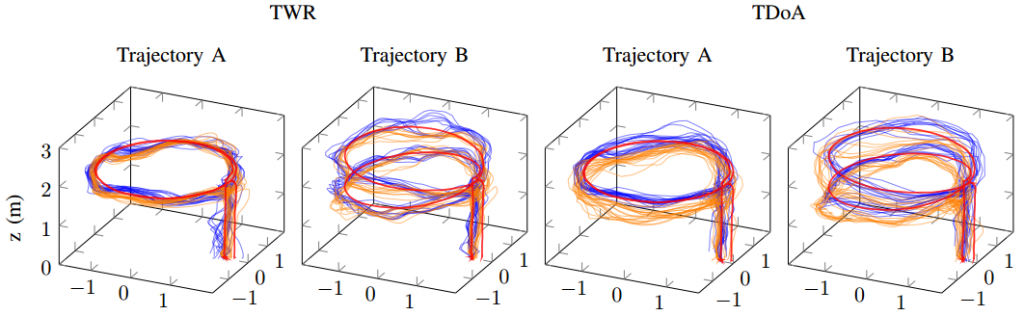
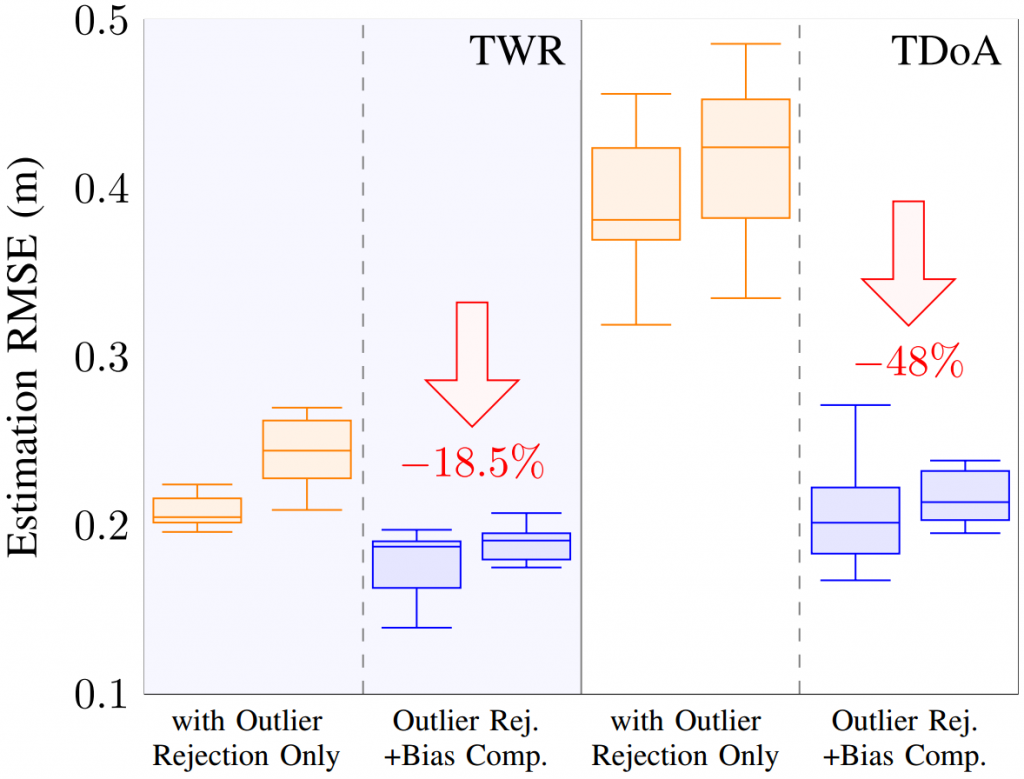
The distributions of the RMS estimation errors are summarized into a box plot. TWR-based ranging results in better localization performance than TDoA. However, we observe that, with our neural network bias compensation, the average RMS error of TDoA localization is around 0.21m, which is comparable to that of TWR-based localization (~0.19m). Thanks to the neural network bias compensation, the average reduction in the RMS error is ~18.5% and 48% for TWR and TDoA, respectively. Most notably, this result suggests that bias compensation might help closing the performance gap between TWR- and TDoA-based localization.
Outlook
In this work, we presented a two-step methodology to improve UWB localization—for both TWR- and TDoA-based measurements. We used a lightweight neural network to model and compensate for pose-dependent and spatially-varying biases and an outlier rejection mechanism to filter spurious measurements. Through several real world flight experiments tracking different trajectories, we showed that we are able to improve localization accuracy for both TWR and TDoA, granting safer indoor flight. In our future work, we will include the anchors’ pose information to allow our method to further generalize to previously unobserved indoor environments, with different anchor configurations.
Links
- Video: https://youtu.be/dGMV_l8UC_0
- Paper: https://arxiv.org/abs/2003.09371
- Our Lab: http://www.dynsyslab.org
The authors are with the Dynamic Systems Lab, Institute for Aerospace Studies, University of Toronto, Canada, and affiliated with the Vector Institute for Artificial Intelligence in Toronto.
Feel free to contact us if you have any questions or ideas: wenda.zhao@robotics.utias.utoronto.ca. Please cite this as:
<code>@article{wenda2020learning,
title={Learning-based Bias Correction for Ultra-wideband Localization of Resource-constrained Mobile Robots},
author={Wenda Zhao and Abhishek Goudar and Jacopo Panerati and Angela P. Schoellig},
journal={arXiv preprint arXiv:2003.09371},
year={2020}
}</code>