A state estimator turns sensor signals into an estimate of the state that the crazyflie is in. This is an essential part of crazyflie’s stabilizing system, as explained in the overview page. State estimation is really important in quadrotors (and robotics in general). The Crazyflie needs to know first of all in which angles it is at (roll, pitch, yaw). If it would be flying at a few degrees slanted in roll, the crazyflie would accelerate into that direction. Therefore the controller needs to know good estimate of current angles’ state and compensate for it. For a step higher in autonomy, a good position estimate becomes important too, since you would like it to move reliably from A to B.
Complementary filter
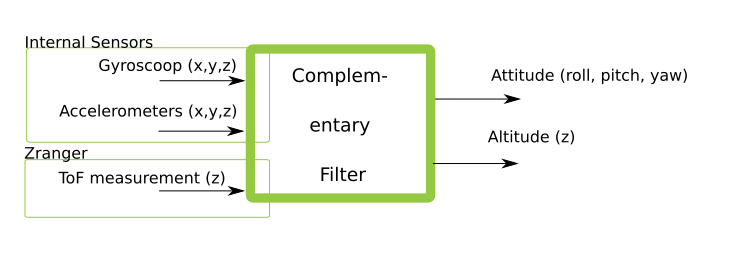
The complementary filter is very lightweight and efficient filter which in general only uses the IMU output of the gyroscope (angle rate) and the accelerometer. The estimator has been extended to also include output of the ToF distance measurement of the Zranger deck. The estimated output is the Crazyflie’s attitude (roll, pitch, yaw) and its altitude (in the z direction). These values can be used by the controller and are meant to be used for manual control.
To checkout the implementation details, please look the firmware in estimator_complementary.c and sensfusion6.c. The complementary filter is set as the default state estimator on the Crazyflie firmware, unless a deck is mounted which requires the Extended Kalman filter.
Extended Kalman filter

The (extended) Kalman filter (EKF) is step up in complexity compared to the complementary filter, as it accepts more sensor outputs of both internal and external sensors. It is a recursive filter that estimates the current state of the Crazyflie based on incoming measurements (in combination with a predicted standard deviation of the noise), the measurement model and the model of the system itself.
We will not go into detail on this but we encourage people to learn more about EKFs by reading up some material like this.
Because of more state estimation possibilities, we prefer the EKF for certain decks that can provide information for full pose estimation (position/velocity + attitude). These are: Flowdeck v2, Loco positioning deck, Lighthouse deck, Mocap deck passive / active. The estimator preferences of these decks are set in their deck api.
Here we will explain a couple of important elements that are essential to the implementation, however we do encourage people also look into the code estimator_kalman.c and kalman_core.c. Also read the papers [1] and [2] for implementation details.
Kalman supervisor
The Kalman filter has a supervisor that resets the state estimation if the values get out of bounds. This can be found here in kalman_supervisor.c.
Measurement Models
This section will explain how the signals of the sensors are transformed to state estimates. These equations are the base of the measurement models of the EKF.
Flowdeck Measurement Model
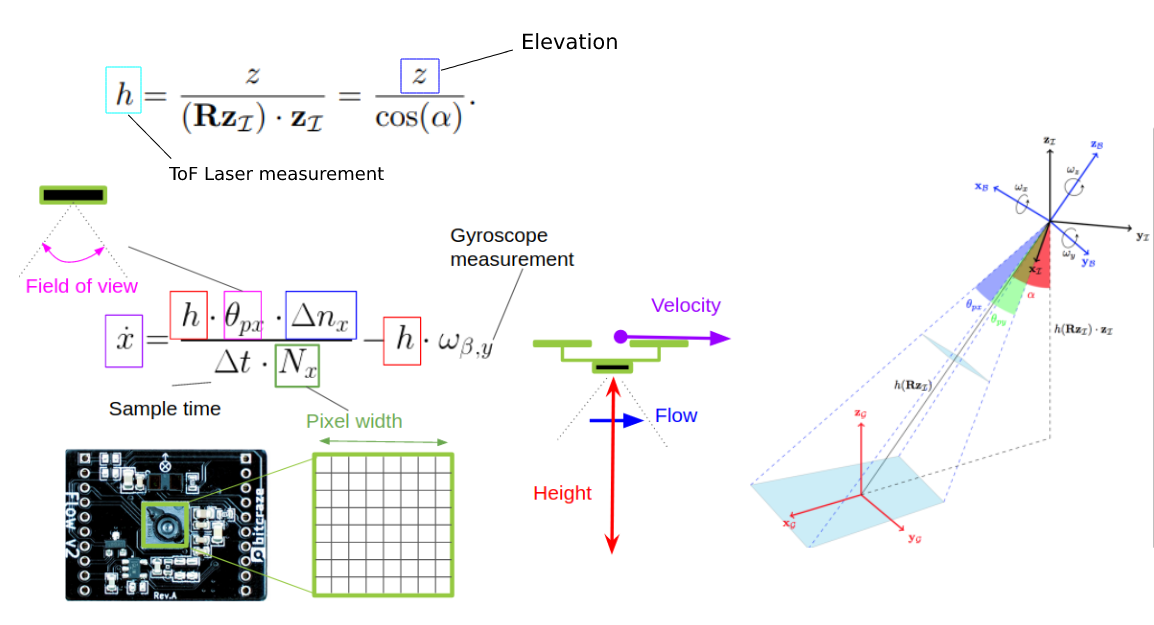
This illustration explains how the height from the VL53L1x sensor and flow from the PMW3901 sensor are combined to calculate velocity. This has been implemented by the work of [3] and can be found in kalman_core.c in the function kalmanCoreUpdateWithFlow() for the velocity and in mm_tof.c for the height.
Unscented Kalman Filter
NOTE This is still in the experimental phase, so it would need to be enabled in kbuild in ‘Controllers and Estimators’ and Enable error-state UKF estimator’
The error-state unscented Kalman Filter (error-state UKF) is another navigational algorithm for the Crazyflie whose objective is improving navigation quality when relying on the Loco-Positioning system. It combines a strapdown navigation algorithm [4] performing a time integration of the accelerometer and gyrosope measurements with an unscented Kalman-Filter estimating the error-state between the strapdown navigation solution and the true position by means of the deck measurements. Just like the EKF described above the UKF is a recursive filter. However, compared to an EKF approach, the UKF does not rely on linearizing the nonlinear measurement equations but instead employs deterministically chosen sigma-points to approximate the mean and the covariance of the error-state. This enhances the approximation accuracy, which turns out to be particularly advantageous when using the Loco-Positioning-System for absolute positioning. The algorithm is described in more details in reference [5]. Further details on deriving error-state predictions models as well as more detailed derivation of the UKF approach can be found in [6] and [7].
In its current implementation, the algorithm is able to fuse the following measurements:
- Loco-Positioning Time difference of arrival (TdoA)
- Flow-Deck v2
The time-of-flight measurements of the flow-deck are also subject to a simple outlier rejection scheme, allowing the Crazyflie to pass over ground obstacles without causing height jumps. The default parameterization consideres a Crazyflie 2.1 quadcpopter fusing Loco-Positioning and/or Flow-Deck measurements. When solely fusing Flow-Deck measurments, the quality gate for time-of-flight measurments (Parameter “ukf.qualityGateTof”) has to be increased.
References
[1] Mueller, Mark W., Michael Hamer, and Raffaello D’Andrea. “Fusing ultra-wideband range measurements with accelerometers and rate gyroscopes for quadrocopter state estimation.” 2015 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2015.
[2] Mueller, Mark W., Markus Hehn, and Raffaello D’Andrea. “Covariance correction step for kalman filtering with an attitude.” Journal of Guidance, Control, and Dynamics 40.9 (2017): 2301-2306.
[3] M. Greiff, Modelling and Control of the Crazyflie Quadrotor for Aggressive and Autonomous Flight by Optical Flow Driven State Estimation, Master’s thesis, Lund University, 2017
[4] D.H. Titterton, J.L. Weston, “Strapdown Inertial Navigation Technology - Second Edition”, Institution of Electrical Engineers, 2004
[5] Kefferpütz, Klaus, McGuire, Kimberly. “Error-State Unscented Kalman-Filter for UAV Indoor Navigation”, 25th International Conference on Information Fusion (FUSION), Linköping, Schweden, 2022
[6] J. Sola, “Quaternion kinematics for the error-state Kalman filter”, arXiv:1711.02508, November 2017
[7] S.J. Julier, J.K. Uhlmann, “A New Extension of the Kalman Filter to Nonlinear Systems“, Signal Processing, Sensor Fusion, and Target Recognition VI, Aerosense 97, Orlando, USA, 1997